Learning to sort
I kind of procrastinate over starting to learn about sorting whenever I am preparing for interviews. Mainly because we need to memorize the working of various sorting algorithms. But over time, I have realized that each sorting algorithm is based on some intuition and if we can understand those intuitions, then it becomes easy to remember how they work.
A fair-warning: This blog post doesn’t contain many images, animations, etc. Just a bunch of text, math, and code - the minimum things just enough for me to get ideas about sorting whenever I feel like!
One of my earliest attempts at learning about sorting algorithms is by writing machinepack-sort
I am going to do a similar effort here, but this time I am planning to do these steps.
- Understand and visualize how a sorting algorithm works. (by reading blogs, seeing video tutorials and lectures)
- Come up with the time and space complexity for each of them.
- Write code and test the implementation using this leetcode puzzle
- Try to find practical use cases for each algorithm. (in the retrospect, wasn’t able to concentrate on this much. Maybe I will update this post, as I discover a usage in a practical use case)
There are just a lot of different sorting algorithms. This blog contains the most common ones at first and is open to get updated with some more sorting algorithms as I learn/discover them.
Preface
I will try to collect information that might clarify details for understanding the sorting algorithms in this section.
Trade-off
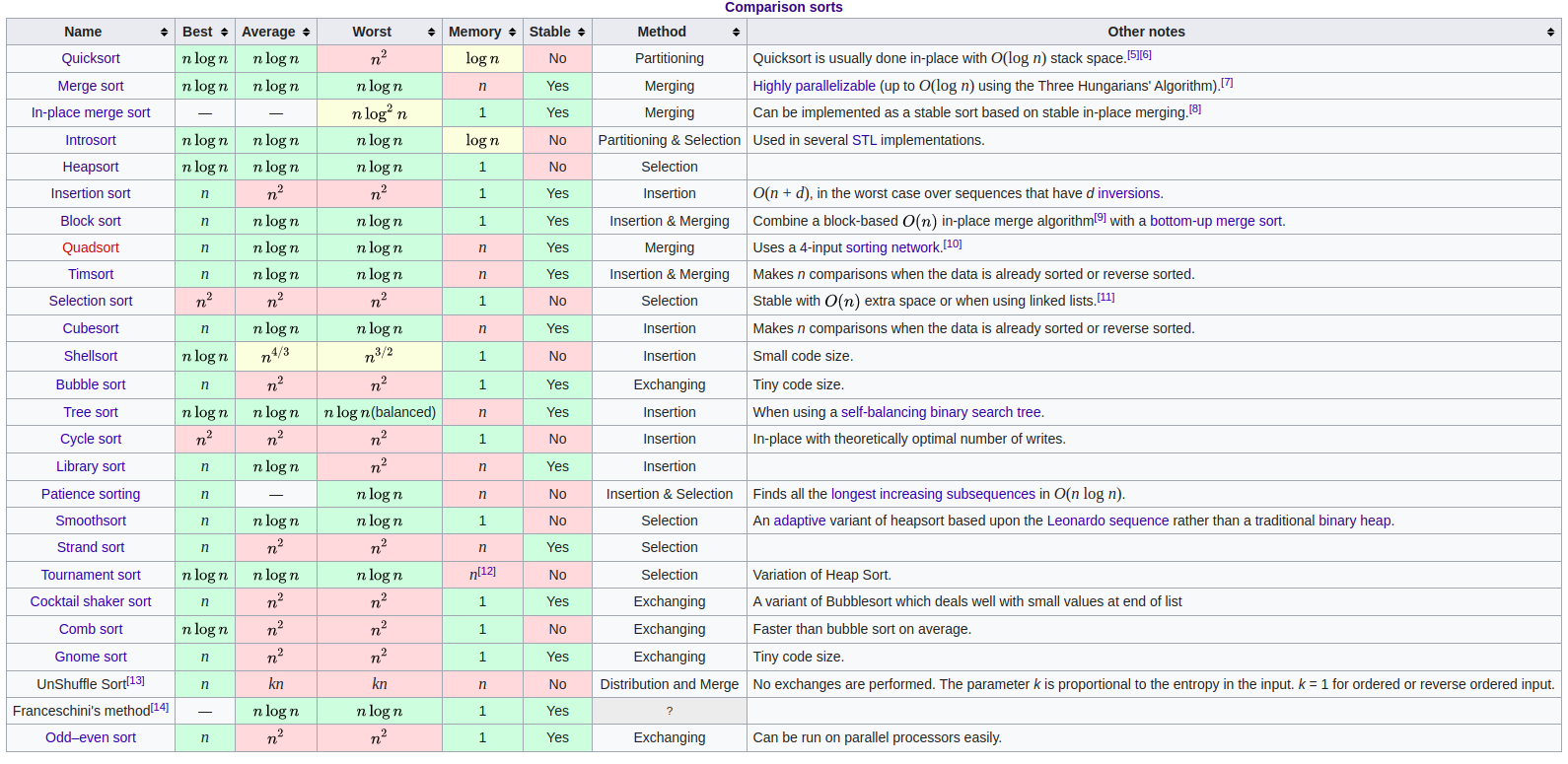
I heavily recommend taking a look at this comparison table to understand the trade-offs of different kinds of sorting algorithms.
Pasting a screenshot of the table here. One could use this table to compare and contrast different algorithms and reason about which one to use!
0,1
I think it is good to think about the very basic cases first and handle them at first. The very basic case is
When the list to be sorted has only one or zero elements, we just have to return the list itself (because it is already sorted)
1 | func sortArray(nums []int) []int { |
I think that some implementations try to embed this logic in the core logic itself, but anyway I would just like to make things simple and take one thing off from our table right away!
Stable Sorting
When sorting a collection, what if two items with the same value exist.
[5 2 1 1 6]
Notice how 1 is repeated. While sorting, should we leave their relative order the same or should we shift them?
Well, it is up to you. If your sorting implementation maintains the relative order of equal elements, then it is said to be stable sorting.
Here is a more practical example. Consider an array of JSON objects that need to be sorted based on marks of students.
1 | [ |
If the above array is to be sorted using stable sorting, we would get
1 | [ |
In case of an unstable sort, we might get
1 | [ |
Notice how the relative order of two persons with the same mark is disrupted for an unstable sort.
Further reading: https://en.wikipedia.org/wiki/Sorting_algorithm#Stability
Comparison and non-comparison sorts
Woah, just discovered this type of categorization of sorting algorithms: https://en.wikipedia.org/wiki/Sorting_algorithm#Comparison_of_algorithms
I think for most of the post here we will focus on Comparison sorts but would like to explore this topic as we explore various algorithms.
Sorting Algorithms
Selection Sort
A very simple sorting technique. The reason it is called a selection sort is that we will select the lowest/highest element at a time and place it in a sorted manner.
I think this example from Wikipedia makes it clear
| Sorted sublist | Unsorted sublist | Least element in unsorted list |
|---|---|---|
| () | (11, 25, 12, 22, 64) | 11 |
| (11) | (25, 12, 22, 64) | 12 |
| (11, 12) | (25, 22, 64) | 22 |
| (11, 12, 22) | (25, 64) | 25 |
| (11, 12, 22, 25) | (64) | 64 |
| (11, 12, 22, 25, 64) | () |
Intuition
So the intuition here is to select the lowest/highest number from the unsorted sublist and move it to sorted sublist.
Time Complexity
Finding the the lowest/highest element takes O(n). This search needs to be done n times in-order to get the final answer.
The number of items to be searched decreases by one each time. First we search n items, then (n-1) items:
n + (n-1) + (n-2) + …. + 1
Now it boils to simple math, “Sum of first n natural numbers” = (n*(n+1))/2 = (n2 + n) / 2
Now omitting the constants and lower degree, we arrive at the time complexity.
O(n2)
Space complexity
We move the lowest/highest element each time to a sorted sublist. The space complexity really depends on the way we allocate this sorted sublist.
If we create a new list and append the lowest/highest each time, then we will end up with n allocations. So O(n).
But if we implement our code in a way to just swap the (n-1)th index for the nth lowest/highest element, we would end up doing everything in-place. So O(1).
Step by step code
First we try to write down the logic for finding the lowest number (assume we need to do ascending order sort).
1 | func findSmallest(nums []int) int { |
If we execute this n times, we will get back the same index. Our idea here is to reduce the length of the unsorted sublist being passed into the array, so that we get back the index of nth lowest item. So building up on that.
1 | func findSmallest(nums []int, start int) int { |
Now, we just call the findSmallest procedure n times and do a swap everytime to construct the sorted sublist.
1 | func sortArray(nums []int) []int { |
Full code
Now, we have a Space = O(1) and Time = O(n2) implementation here!
1 | func sortArray(nums []int) []int { |
Resources
Bubble Sort
Values are bubbled up while sorting using Bubble sort. Lets see what we mean by “bubbling up”.
The way bubble sort works is, we compare i and i+1 elements and swap them if ith element is greater than (i+1)th element. If we do this repeatedly for ~n times, the greater elements would start bubbling up at the end of the list and the list will be sorted at the end.
Consider the example of sorting: [5, 4, 6, 2, 1] (into an ascending order list)
i=0; First we compare 5 and 4. Since 5 > 4, we swap.
4 5 6 2 1
i=1; We compare 5 and 6. Since 5 < 6, no swap.
4 5 6 2 1
i=2; We compare 6 and 2. Since 6 > 2, we swap.
4 5 2 6 1
i=3; We compare 6 and 1. Since 6 > 1, we swap.
4 5 2 1 6
That’s it! Notice how 6 (the highest number) got bubbled up at the end of the list.
If we perform the same procedure n times, we will end up bubbling all the n highest numbers, thus resulting in sorted order.
Intuition
Bubble up the highest number to the last and build up the sorted list from backwards.
Time Complexity
We are performing in-memory swaps upto the n-1th index in the first iteration. At this point, the highest number is bubbled up at the n-1th index.
In the second iteration, we perform swapping upto the n-2th index. At this point, the highest number is bubbled up at the n-2th index.
This iteration happens n times and for each iteration the length of the unsorted list goes down by one.
n + (n-1) + (n-2) + …. + 1
Again it boils to simple math, “Sum of first n natural numbers” = (n*(n+1))/2 = (n2 + n) / 2
Now omitting the constants and lower degree, we arrive at the time complexity.
O(n2)
Space Complexity
This is easy to figure out because we are not allocating any new structures during the process. We are just doing a bunch of in-memory swaps.
So, O(1)
Step by step code
First, we will handle for the case where array is of size 0 or 1. In that case, we just need to return back the same array.
1 | func sortArray(nums []int) []int { |
Now, we will try to get the “bubble up” code done. This part of the code will just bubble the highest element. Once we have this logic, we just perform the logic for n times to bubble up all the elements.
1 | for i := 0; i <= (len(nums)-2); i++ { |
Cool, we will wrap up the bubble up code with a loop running n times.
1 | for n := 0; n < len(nums); n++ { |
That’s it, we should now have nums sorted in-memory. We can try to do one optimisation here. Since we bubble up the highest element, we can avoid trying the swapping logic on already bubbled up values. So, instead of iterating up to len(nums)-2 index, we will iterate up to (len(nums)-2)-n) index, so that we avoid the index of already bubbled up values.
1 | for n := 0; n < len(nums); n++ { |
Full code
1 | func sortArray(nums []int) []int { |
Resources
Insertion sort
At first, it felt similar to selection sort and made me wonder what actually is the difference between them.
I would say that insertion sort is little bit intelligent than both of the above algorithms: selection sort and bubble sort. This is because when we feed an already sorted array or an almost sorted array to those algorithms, they don’t understand that it is an already/almost sorted array and run for O(n2) time, no matter what.
But in that case, insertion sort seem to run just for O(n) time. This video gave an example of where we might get an already/almost sorted database: think of a database where keys are already sorted.
Intuition
Given an array, consider the first element to be sorted already. Start from the next element and insert it at the right position in the sorted array. If the element is already in the right position of the sorted array, we just move to the next position.
(I recommend you to watch the video resources below to get more idea about this technique)
Time complexity
Worst and Average case: O(n2) because it would take (n(n+1))/2 swaps in these cases.
Best case: When the array is already sorted, insertion sort just takes O(n) times. If you compare this with selection sort and bubble sort, they both take O(n2). Hence insertion sort is a better choice.
Space complexity
Swaps are done in-place.
So O(n)
Step by step code
First we start with the second item in the array.
1 | for i := 1 ; i < len(nums); i++ { |
Now, we just insert the i-th element at the right place of the array.
1 | for i := 1 ; i < len(nums); i++ { |
Full code
1 | func sortArray(nums []int) []int { |
Resources
- CS50 Insertion sort
- :star: San Diego State University - Rob Edwards - Insertion Sort
- Insertion Sort Wikipedia
Merge sort
Merge sort is a good example for divide and conquer algorithm. It is easy to solve this problem by thinking in recursion. To give a mental model of what a merge sort looks like, I am going to use a nice picture that I found in Wikipedia
Found this insight in The Algorithm Design Manual book,
Mergesort is a great algorithm for sorting linked lists, because it does not rely on random access to elements as does heapsort or quicksort.
Intution
Split the array to be sorted into two, sort those individually, and merge them back together. Repeatedly apply this on the divided arrays. When the divided array has only one element, it is already sorted. (That’s the point where we stop splitting and merging back starts!)
Time complexity
Recommending the MIT 6.006 Merge Sort video to figure out how this is done.
At each level of splitted arrays, we access n items and we would have a total of log n levels. Hence, time complexity is O(n log n)
Space complexity
I tried implementing merge sort with the help of “Top Down Split Merge” + “Two queues” like mentioned in The Algorithm Design Manual book. I think the space for this method is also O(n log n).
But if we follow the algorithm where we use a temporary array instead of allocating two queues everytime , we can get an O(n) space complexity.
Step by step code
We will try to code the temp array method here! Two queue method is relatively easy. You should try doing the two queue method first if you are not sure. (I have provided the two queue technique in the full code section below.
Prepare for a recursive ride! haha. Merge sort has two parts: Split and Merge (remember the diagram).
first, we make a temporary array (which we use to merge) and call merge sort procedure from index 0 to n-1.
1 | func sortArray(nums []int) []int { |
The ms call does the split. then we call a merge function to perform the merge.
1 | func ms(nums, temp []int, low, high int) { |
Now the merge part:
1 | func merge(nums, temp []int, low, mid, high int) { |
The thing that I miss out is the last section of the merge where we copy the temp array to the source array.
Full code
Two queues
1 | func sortArray(nums []int) []int { |
Temporary array
1 | func sortArray(nums []int) []int { |
Resources
- Merge Sort Wikipedia
- MIT 6.006 Merge Sort
- The Algorithm Design Manual Book
- :star: San Diego State University - Rob Edwards - Merge Sort (Despite the black screen problem in the video, I still think the video did a good job of explaining the merge part)
Quick sort
Quicksort is one of the sorting algorithms that I have noticed in practice often. For example, I remember noticing QSORT while reading git’s source code on how git suggests commands when we make a mistake while typing a git command.
Also, I have read that quick sort seems to be a choice for standard library implementation of sorting in some programming languages. Example: Go’s sort package
There are different flavors of qsort and one needs to consider the tradeoffs to choose the one that suits their needs. For example, Lomuto Partition Scheme chooses the pivot point as the last element of the array and performs qsort, whereas
Intuition
Choose a pivot point (probably the last element of the array) and partition lesser and higher elements based on the pivot. Perform the pivot and partition logic recursively for the partitions.
Time complexity
If the pivot point we choose is approximately the middle of the sorted list, then the list is divided equally (like merge sort). So quick sort has a time complexity of O(n log n) for the best and average case.
For the worst case, (where we choose the pivot point as the first or last element of the sorted array as the first pivot), the algorithm performs O(n2).
Space complexity
For the best and average case, the space complexity would be (log n) (because of the call stack used for recursion). In the worst case, that would become O(n)
Step by step code
First, we write the recursive logic of partition and qsort.
1 | func qsort(nums []int, low, high int) { |
Next, we implement the partitioning logic. I am using the Lomuto Partition Scheme here.
1 | func part(nums []int, low, high int) int { |
Full code
1 | func sortArray(nums []int) []int { |
Resources
- :star: Quick sort Wikipedia
- San Diego State University - Rob Edwards - Quick sort
- San Diego State University - Rob Edwards - Quick sort worst case
- San Diego State University - Rob Edwards - Quicksort code
Heap sort
The most important idea behind heap sort is to first build a heap out of the given array. A heap is just a common way of implementing a priority queue. A priority queue is just a data-structure, where we could request for an element with either the largest or smallest priority at a given point of time.
With that Intuition, the implementation could be pretty simple. Consider a language with a priority queue implementation built into the standard library like C++. In this case, we could write something like,
1 | class Solution { |
We just create a min-heap and extract the minimum element each time and append it to a list. While this approach involves allocating space, there is a way to achieve this in-memory if the input is an array.
Intuition
Construct a max-heap and pick the largest element using it, one at a time to fill it at the end of the sorted list.
Time complexity
I recommend watching the MIT 6.006 Heaps and Heap sort lecture for deriving the time complexity. It seems like building a heap from scratch is O(n) and extracting a min/max element seems to be O(log n) since we extract the min/max n times, the time complexity would be O(n log n)
Space complexity
A naive implementation of constructing a priority queue from scratch (like with standard library code or any other library) might lead to O(n).
But we will be using a binary heap (just represented in-place in the given array), there is no extra space allocated. So the space complexity would be O(1).
This might seem to be the best algorithm so far, but there should be something that we are losing, right? It is the stableness. Seems like heap sort is not stable.
Step by step code
We need to learn and remember about a few array-tree math before trying to code it. First binary heaps are array representation of a binary tree.
[0 1 2 3 4]
Value at 0 is the root node. values at 1 and 2 are children of the root node (0). The children of 1 would be 3 and 4.
This leads to arriving at the following formulae.
the left child of a node at index i is given by (2 * i) + 1 and right child of a node at index i is given by (2 * i) + 2.
If there are n nodes, (n/2) - 1th index will give the node whose children will all be leaf nodes. This is a very useful insight that I got from MIT 6.006 Heaps and Heap sort. This means that, since its children are leaf nodes, they already satisfy the heap property and it might be the right place to start recursion procedure for building up the heap from bottom up.
Ok, let’s start writing this! First, we call the heapify procedure from (n/2)-1th index to 0th index
1 | for i := (len(nums)/2) - 1; i >= 0; i-- { |
With this, the root node is guaranteed to have the largest element. So, we start filling up the array from back by extracting the max element. Every time we extract the max element, the heap becomes dirty. So we could just call heapify for only the unsorted sub-array at the beginning.
1 | for i := len(nums)-1; i >= 0; i-- { |
Ok, now we start implementing the heapify function.
1 | func heapify(nums []int, n, idx int) { |
Full code
1 | func sortArray(nums []int) []int { |
Resources
- MIT 6.006 Heaps and Heap sort
- GeeksForGeeks solution (this closely follows the ideas behind the MIT 6.006 lecture)
More
Leaving the space for this blog post to get updated. Some interesting sorting algorithms to watch out for are
- BST sort
- AVL sort
- Shell sort
- Counting sort
- Radix sort
( you tell me )